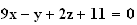1) Réponse : a
Soit
G le barycentre de
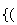A
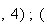B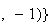
Ce
barycentre existe car
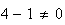
De plus pour tout point M du plan , on a la relation suivante :
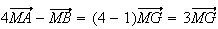
Donc
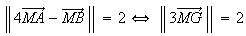
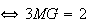
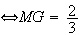
L'ensemble
des points M de l'espace tel que
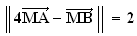est
donc la sphère de centre G de rayon
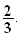
2) Réponse : c
H
de coordonée
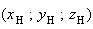est le projeté ortogonal du point A sur le plan
.
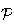Donc
le vecteur
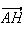est colinéaire au vecteur normal du plan
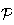de coordonée (1 ; 2 ; 2)
Il
existe donc
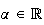tel que :
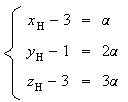
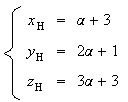
De
plus H
.
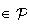Les coordonées de H vérifient dnc l'équation du plan
:
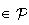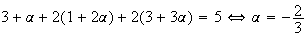
Finalement on a :
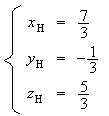
On
a donc
H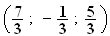
3) Réponse : c
Rappel
: Etant donné un plan
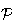d'équation
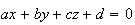et un point
M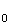
de coordonée
(x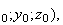
la
distance de
M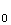
à
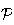s'écrit :
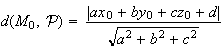
Ici
la position de la sphère de centre B et de rayon 1 par rapport au plan
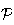est déterminée par la distance du point B au plan
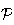. Calculons donc cette distance :
.
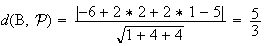Cette
distance étant supérieure au rayon 1 de la sphère, la
sphère ne coupe pas le plan
.
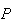4) Réponse : c
Les
droites
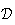et
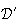ont respectivement pour vecteurs directeurs
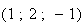et (2 ; 1 ; 1). Ces vecteurs n'étant pas colinéaires, les droites ne
sont pas parallèles.
La
droite
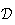est la droite passant par A et de vecteur directeur
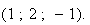
Elle
a donc pour équation paramétrique
:
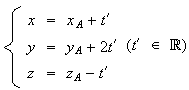
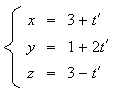
Les
droites
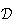et
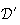sont sécantes s'il existe
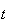et
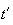tels que :
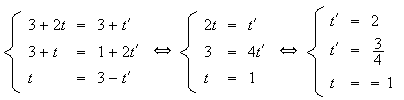
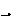impossible : Ce système n'admet pas de solution.
Les droites ne sont pas sécantes
Finalement les droites ne sont ni sécantes, ni parralèles , elles sont donc non coplanaires.
5) Réponse : b
L'ensemble
des points M de l'espace équidistants de A et B est le plan
médiateur de [AB] passant par I milieu de [AB] avec I qui a pour
coordonée
.
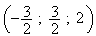Le
vecteur
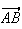de coordonée
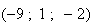est un vecteur normal à ce plan. et les points M vérifient :
.
.
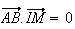
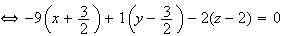
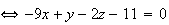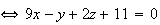L'ensemble
des points M de l'espace équidistants de A et B est donc le plan
d'équation cartésienne :
