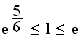CORRIGE MATHEMATIQUES Centres étrangers
SECTION S - JUIN
2005
Partie A :
1)
f et g sont dérivables sur
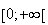comme somme de 2 fonctions dérivables et pour tout
,
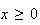on a :
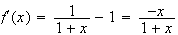
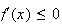car
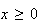
Donc
f est décroissante sur
.
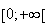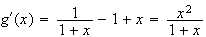
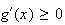
Donc
g est croissante sur
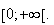
2)
On a
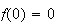et f décroissante sur
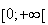(d'après 1) donc f est négative sur
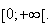
soit
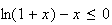
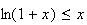
De
même on a
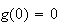et g croissante sur
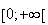donc g est positive sur
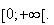
soit
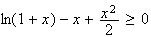
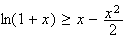
Finalement
pour tout
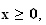on
a :
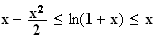
Partie B :
1)
Montrons par récurrence que pour tout n
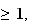u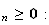
n=1
:
u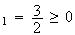
OK
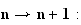
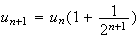
Or
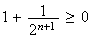
De
plus par hypothèse de récurence, on
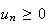
Donc
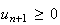
Conclusion :
Donc
pour tout n
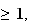u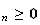
2)
Montrons par récurence que pour tout
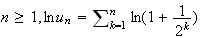
n=1:
u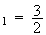
ln(u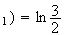
Or
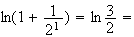ln(u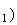
Donc la proposition est vrai au rang 1
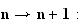
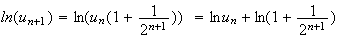
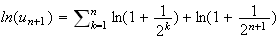
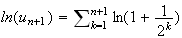
CQFD
Conclusion :
Pour
tout
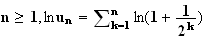
3)
D'aprés la question 2 Partie A, on a pour tout
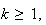en prenant
x=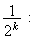
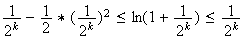
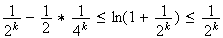
En sommant l'inégalité précédente en faisant varier k de 1 à n, on obtient :
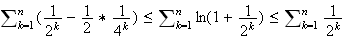
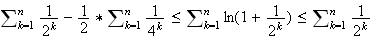
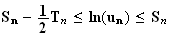
4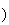
Sn est la somme de termes de suites géométriques de raison
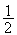
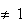
S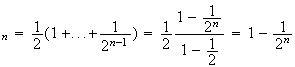
Donc
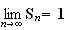car
(
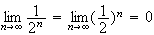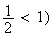
De
même
T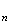
est la somme de termes de suite géométrique de raison
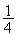
T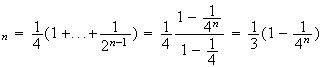
Donc
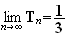car
(
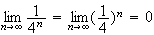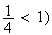
5)a)
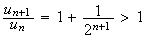
Donc
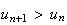
La
suite
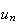est strictement croissante.
b) D'après la question 3 on a :
ln(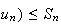
Or
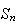est croissante et
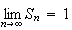donc
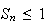
Donc
ln(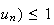
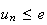
Donc
la suite
(
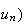est majorée
De
plus on sait d'après la question 5)a) , que la suite
(
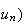est croissante.
Donc
la suite
(
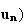converge.
On appele l sa limite.
c) On a vu précedement que :
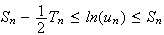
On passe à la limite dans l'inégalité précédente.
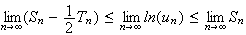
1-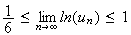
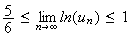
Or
comme la suite est croissante et à termes strictement positifs, on a l
> 0 .La fonction ln est continue en l donc
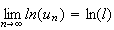
d'où :
